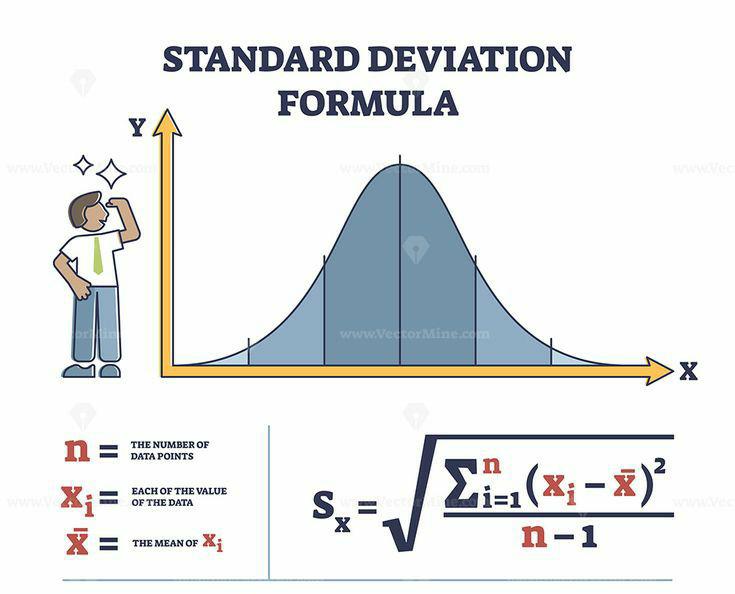
Introduction about Standard deviation
Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a dataset. It is widely used in various fields, including mathematics, statistics, finance, and scientific research. Understanding how to calculate standard deviation is essential for analyzing and interpreting data accurately. In this article, we will provide a step-by-step guide on calculating standard deviation, ensuring that you grasp this fundamental concept.
Table of Contents
ToggleWhat is Standard Deviation?
Standard deviation measures the spread of data points around the mean (average) of a dataset. It indicates the degree to which individual data points deviate from the mean. A low standard deviation suggests that the data points are closely clustered around the mean, while a high standard deviation indicates a wider spread.
Thanks for the video The Organic Chemistry Tutor!
Step-by-Step Guide to Calculating Standard Deviation:
Step 1: Find the Mean
Calculate the mean of the dataset by summing all the values and dividing by the total number of data points. The formula for calculating the mean is:
Mean = (sum of all values) / (total number of values)
Step 2: Calculate the Deviation
Find the deviation of each data point from the mean. To do this, subtract the mean from each individual data point. The formula for calculating deviation is:
Deviation = Data Point – Mean
Step 3: Square the Deviation
Square each deviation obtained in step 2. Squaring the deviations ensures that they are positive values and eliminates any cancellation of positive and negative deviations.
Step 4: Calculate the Variance
Calculate the variance by finding the mean of the squared deviations. The formula for calculating variance is:
Variance = (sum of squared deviations) / (total number of values)
Step 5: Take the Square Root
Finally, take the square root of the variance to obtain the standard deviation. The formula for calculating standard deviation is:
Standard Deviation = √Variance
Example Calculation of Standard deviation
Let’s illustrate the calculation of standard deviation with a simple example:
Dataset: 5, 8, 12, 15, 20
Step 1: Find the Mean
Mean = (5 + 8 + 12 + 15 + 20) / 5 = 60 / 5 = 12
Step 2: Calculate the Deviation
Deviation = [5 – 12, 8 – 12, 12 – 12, 15 – 12, 20 – 12] = [-7, -4, 0, 3, 8]
Step 3: Square the Deviation
Squared Deviation = [49, 16, 0, 9, 64]
Step 4: Calculate the Variance
Variance = (49 + 16 + 0 + 9 + 64) / 5 = 138 / 5 = 27.6
Step 5: Take the Square Root
Standard Deviation = √27.6 ≈ 5.25
Interpretation of Standard Deviation:
The standard deviation obtained from the calculation represents the average amount of deviation from the mean within the dataset. In our example, the standard deviation is approximately 5.25. This indicates that, on average, the data points deviate from the mean by about 5.25 units.
A higher standard deviation suggests a greater degree of dispersion or variability within the dataset. Conversely, a lower standard deviation indicates that the data points are closely clustered around the mean.
Understanding about Standard Deviation
Before diving into the calculation methods, it’s crucial to grasp the concept of standard deviation. Standard deviation measures the average deviation or distance of individual data points from the mean. A high standard deviation indicates a wide spread of data points, suggesting a greater degree of variability or dispersion. Conversely, a low standard deviation indicates that the data points are closely clustered around the mean.
Now, let's explore some tips and tricks that will help you master standard deviation and make the most out of your data analysis endeavors.
- Data Cleaning and Preparation
Before calculating standard deviation, it’s crucial to ensure that your dataset is clean and properly prepared. Remove any outliers or erroneous data points that may significantly affect the results. Outliers can skew the mean and subsequently impact the standard deviation. By conducting thorough data cleaning and preparation, you can ensure that your calculations are based on reliable and accurate information.
- Consider the Data Distribution
Understanding the distribution of your data is vital when interpreting the standard deviation. Different types of distributions, such as normal, skewed, or multimodal distributions, can have distinct impacts on the standard deviation. For example, in a normal distribution, approximately 68% of the data falls within one standard deviation of the mean. Being aware of the underlying distribution will help you interpret the standard deviation more effectively.
- Compare Standard Deviations
When comparing data sets or subsets, it’s essential to consider their respective standard deviations. By comparing standard deviations, you can identify variations in the dispersion of data points. A smaller standard deviation indicates less variability, while a larger standard deviation suggests a wider spread. Comparing standard deviations allows you to assess the consistency or inconsistency within different sets of data.
- Utilize Visualization Techniques
Visualizing your data is a powerful way to gain insights into the variability and patterns within your dataset. Create histograms, box plots, or scatter plots to explore the distribution and spread of data points. These visual representations can help you identify any outliers, skewness, or other characteristics that may impact the standard deviation. By combining visualization techniques with standard deviation analysis, you can gain a more comprehensive understanding of your data.
- Consider Sample Size and Bias
The size of your dataset can influence the standard deviation. Smaller sample sizes tend to have larger standard deviations due to the limited amount of data points. Additionally, be mindful of any biases in your data collection process. Biased data may lead to inaccurate standard deviation calculations and misleading interpretations. Take care to ensure your data collection process is representative and unbiased.

Let's dive into the frequently asked Top 30 questions and their detailed answers about Standard deviation
Q1: What is standard deviation?
A1: Standard deviation is a statistical measure that quantifies the spread of data points around the mean.
Q2: How is standard deviation calculated?
A2: Standard deviation is calculated by finding the square root of the variance, which is the average of the squared deviations from the mean.
Q3: What does a high standard deviation indicate?
A3: A high standard deviation suggests a wider spread of data points, indicating greater variability or dispersion within the dataset.
Q4: What does a low standard deviation indicate?
A4: A low standard deviation indicates that the data points are closely clustered around the mean, suggesting less variability.
Q5: How can I calculate standard deviation in Excel?
A5: In Excel, you can use the STDEV function to calculate the standard deviation of a dataset.
Q6: Should I remove outliers before calculating standard deviation?
A6: It is advisable to remove outliers if they significantly affect the results. Outliers can skew the mean and subsequently impact the standard deviation.
Q7: Can standard deviation be negative?
A7: No, standard deviation is always a non-negative value because it involves the square root of squared deviations.
Q8: What is the relationship between standard deviation and variance?
A8: Variance is the squared value of standard deviation. It measures the average of the squared deviations from the mean.
Q9: How does sample size affect standard deviation?
A9: Smaller sample sizes tend to have larger standard deviations due to the limited amount of data points.
Q10: Can I compare standard deviations of different datasets?
A10: Yes, comparing standard deviations allows you to assess variations in the dispersion of data points between different datasets.
Q11: How can I interpret standard deviation in relation to a normal distribution?
A11: In a normal distribution, approximately 68% of the data falls within one standard deviation of the mean.
Q12: What are some common misconceptions about standard deviation?
A12: A common misconception is that standard deviation tells us about the individual data points rather than the variability within the dataset.
Q13: How does standard deviation differ from range?
A13: Range measures the difference between the maximum and minimum values in a dataset, while standard deviation captures the spread of data points around the mean.
Q14: Can I calculate standard deviation for qualitative data?
A14: Standard deviation is primarily used for quantitative data. For qualitative data, other measures, such as mode or frequency, may be more appropriate.
Q15: How can I visualize the standard deviation?
A15: Visualizing your data using histograms, box plots, or scatter plots can help you understand the spread and patterns within the dataset.
Q16: What are some common mistakes to avoid when calculating standard deviation?
A16: Avoid including outliers, using the wrong formula, or misinterpreting the results. Also, ensure your dataset is properly prepared and free from biases.
Q17: How can standard deviation help in decision-making?
A17: Standard deviation provides insights into the variability within a dataset, enabling informed decision-making based on reliable statistical measures.
Q18: Can I use standard deviation to compare different data sets?
A18: Yes, comparing standard deviations can
help identify variations in the dispersion of data points between different data sets.
Q19: How can I reduce the standard deviation of my data?
A19: Reducing the standard deviation requires reducing the variability within the dataset, which can be achieved through data normalization, process improvements, or filtering out outliers.
Q20: Are there alternative measures to standard deviation?
A20: Yes, there are other measures such as mean absolute deviation (MAD) and interquartile range (IQR) that can be used to quantify variability.
Q21: Is standard deviation affected by the scale of measurement?
A21: Yes, the scale of measurement can impact the standard deviation. Therefore, it’s important to consider the context and units of measurement when interpreting results.
Q22: How can I deal with missing data when calculating standard deviation?
A22: Depending on the extent of missing data, you may choose to exclude those observations or use imputation techniques to estimate missing values.
Q23: Can standard deviation be used for non-numerical data?
A23: Standard deviation is primarily used for numerical data. For non-numerical data, other measures such as mode or frequency may be more appropriate.
Q24: Does standard deviation provide information about the shape of the distribution?
A24: No, standard deviation measures the spread of data points but does not provide information about the shape of the distribution.
Q25: How can I communicate the standard deviation to others effectively?
A25: When communicating the standard deviation, provide context, explain its interpretation, and consider using visual aids to aid understanding.
Q26: Are there any software or tools that can calculate standard deviation for me?
A26: Yes, various statistical software packages like R, Python, SPSS, and Excel can calculate standard deviation for you.
Q27: What is the difference between population standard deviation and sample standard deviation?
A27: Population standard deviation is used when calculating the standard deviation for an entire population, while sample standard deviation is used for a subset or sample of the population.
Q28: Can standard deviation be influenced by extreme values?
A28: Yes, extreme values can have a significant impact on the standard deviation, especially when the sample size is small.
Q29: How can I determine if the standard deviation is acceptable for my data?
A29: There is no fixed rule for determining an acceptable standard deviation. It depends on the context, data, and specific analysis goals. Comparing with historical data or industry benchmarks can provide some guidance.
Q30: Can standard deviation be used for time series data?
A30: Yes, standard deviation can be applied to time series data to measure the variability or dispersion of values over time.
Advantages and Tips & Tricks about Standard deviation
- Standard deviation helps measure the spread of data points, providing valuable insights into the variability and distribution of your data.
- Calculating standard deviation allows you to quantify the dispersion within a dataset accurately.
- Understanding standard deviation enables you to make informed decisions based on reliable statistical measures.
- Removing outliers before calculating standard deviation ensures more accurate results.
- Visualizing your data through histograms, box plots, or scatter plots enhances your understanding of the spread and patterns within the dataset.
- Comparing standard deviations between different datasets helps identify variations in the dispersion of data points.
- Considering the distribution of your data is crucial when interpreting the standard deviation.
- Clean and prepare your data by removing erroneous or inconsistent data points to ensure reliable standard deviation calculations.
- Being aware of the sample size’s impact on standard deviation helps you interpret and compare results appropriately.
- Utilize software or statistical tools like Excel, R, or Python to calculate standard deviation efficiently.
- Understanding the relationship between standard deviation and variance helps in data analysis.
- By comparing standard deviations, you can assess the consistency or inconsistency within different sets of data.
- Properly communicating the standard deviation to others requires providing context and explaining its interpretation.
- Using visualization techniques alongside standard deviation analysis provides a more comprehensive understanding of your data.
- Considering the scale of measurement is crucial when interpreting standard deviation results.
- Carefully handle missing data when calculating standard deviation, either through exclusion or imputation techniques.
- Reducing variability within the dataset helps lower the standard deviation.
- Standard deviation is widely used in various fields, including finance, economics, and natural sciences, for meaningful data analysis.
- Standard deviation can be applied to time series data to measure the variability of values over time.
- Comparing standard deviation with historical data or industry benchmarks can provide insights into data performance.
- Understanding common misconceptions about standard deviation helps avoid misinterpretation of results.
- Standard deviation provides a measure of reliability and precision in data analysis.
- Applying standard deviation to quantitative data is more appropriate than using it for qualitative data.
- Standard deviation allows for better decision-making by providing insights into the variability within a dataset.
- It is essential to consider the context and units of measurement when interpreting standard deviation results.
- Standard deviation helps identify outliers that may significantly impact the mean and subsequent calculations.
- Visual aids, such as graphs or charts, can aid in effectively communicating the standard deviation to others.
- Comparing standard deviations between different subsets or samples can provide valuable insights into variations.
- Regularly updating and refreshing your data analysis techniques helps keep your standard deviation results accurate and relevant.
- Continuously monitoring your data analytics and standard deviation calculations allows for ongoing improvement and refinement of your analysis techniques.
Conclusion about Standard deviation
Mastering the calculation and interpretation of standard deviation is crucial for accurate data analysis. By following the step-by-step guide provided in this article and employing the tips and tricks shared, you can confidently analyze and interpret the variability within your dataset. Remember to clean and prepare your data, consider the distribution, compare standard deviations, utilize visualization techniques, and account for sample size and bias. By integrating these strategies into your data analysis workflow, you’ll enhance your ability to draw meaningful insights and make informed decisions based on reliable statistical measures.
